繼續講解算術化，接著上一篇的尾段，講解了電路約束，透過不同條件約束就產出相對應的門。
往下會講一下拉格朗日多項式和插值。

• 注意: 由於小弟不熟悉使用文章中的"加入數字公式"，所以在表示公式的時候，會用圖片形式或簡單的形式表示，請多多見諒，也歡迎大家介紹一些有用的數學公式工具給我使用。

上一篇提到當再新增一條約束後的矩陣Q表格會是這個: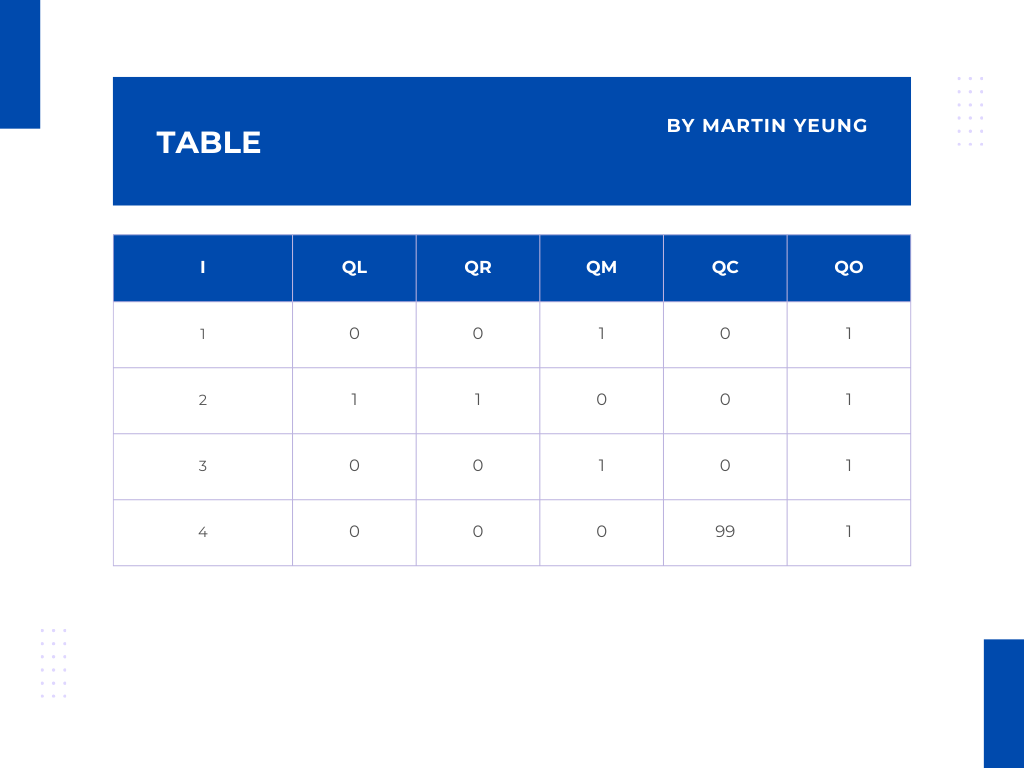

拉格朗日多項式和插值

當拉格朗日插值需要滿足QL[0,1,0,0]時，即f(0)=0, f(1)=1, f(2)=0, f(3)=0 ，可以分別得到以下拉格朗日基本多項式:

相信大家都會有一個很大的疑問，為什麼在以上公式中都加入一個奇怪的常數? 而它由是從何而來?
首先，由於有限域是101，所以在公式運算中都涉及到101的有限域的限制，而這個有限域必須是質數。
第二，以第一條公式為例，分母是-6，在分母轉換時，通過有限域101的限制進行變換(因為 101 mod -6 = -1)而得出84的值。
同樣，在其他公式也需要通過有限域101的限制進行變換，最終會得出相對應的值用於拉格朗日基本多項式。
大家可以嘗試動動手算一下，詳細解說會在往後再加以說明，因為這篇文章是想大家對拉格朗日的原理及操作有基礎認識。

• 將以上公式會進行連結及在滿足QL[0,1,0,0]之下變成最終的拉格朗日插值式為:

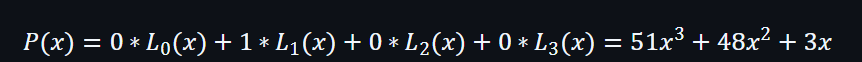
再回到個矩陣W: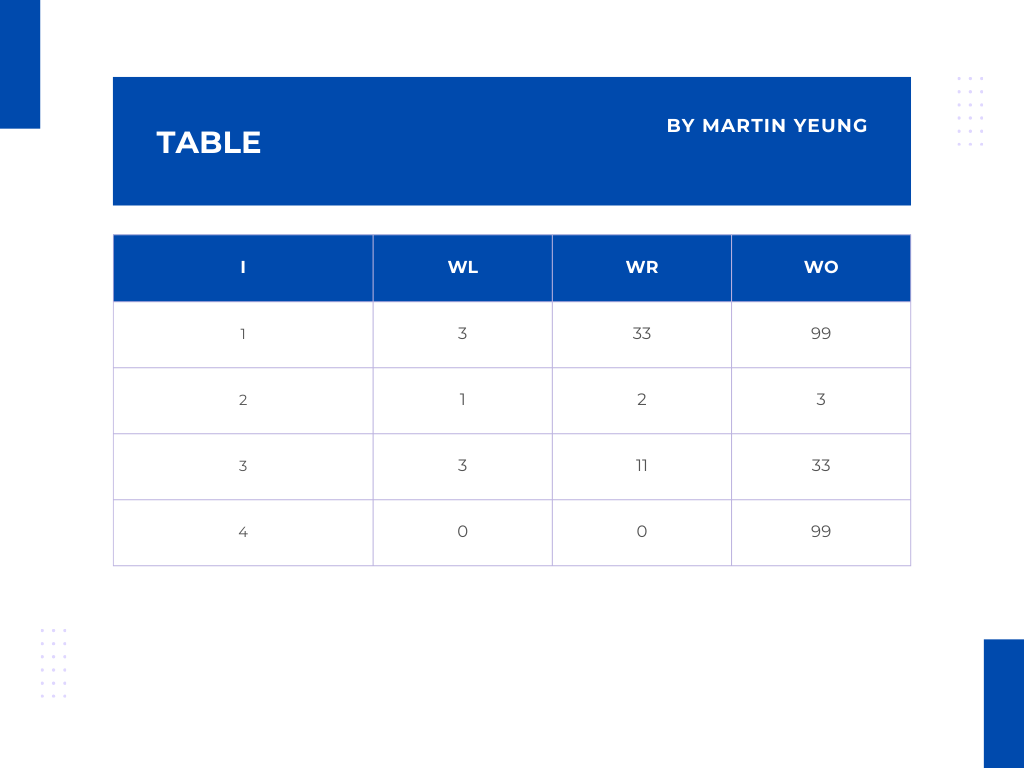

當拉格朗日插值需要滿足WL[3,1,3,0]時，即f(0)=3, f(1)=1, f(2)=3, f(3)=0 .

• 最終的拉格朗日插值式為:

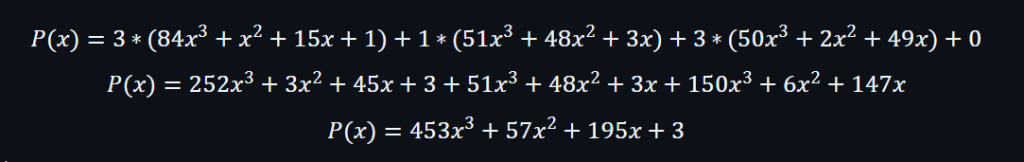
所以: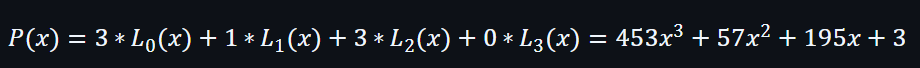

換言之，要滿足WL[3,1,3,0]，就必須在f(0)=3, f(1)=1, f(2)=3, f(3)=0時通過以上多項式。
大家有時間也可以算一算其他約束條件的多項式。

參考資料:

1. Lagrange_polynomial
   https://en.wikipedia.org/wiki/Lagrange_polynomial